起因

前段时间在群里看到群友想要复刻ChatGPT的语音对话效果，手痒之下自己也来复刻一波！

难点解析

这个效果平心而论是比较复杂的，我一般会把这种比较复杂的效果简单拆解出来，然后一步一步来解决。

不规则圆形，可以看到最开始时是由一个圆形过渡到不规则的圆形同时有一个滚动的效果。

溶解粘滞效果，从不规则的圆形过渡到音柱时可以看到有一个粘滞溶解的效果。

音柱的抖动效果，我们需要模拟收音时的不规则抖动效果来更贴近真实场景。

融合拓展效果，从音柱变回圆形的时候，有一个融合的效果让过渡更显丝滑。

神兵利器

在正式开始本篇内容之前我们需要先了解一些解决上述问题的神兵利器。

svg滤镜

SVG滤镜（Scalable Vector Graphics Filters）是SVG（可缩放矢量图形）规范的一部分，用于对SVG图形应用各种视觉效果。SVG滤镜允许开发人员和设计师创建复杂的图形效果，比如模糊、阴影、颜色变化等，而无需使用位图图像
正弦曲线

正弦曲线是一种周期性波动的数学曲线，常用于描述周期性变化的现象，如声波、光波、电磁波、潮汐等。它在数学上被定义为一个角的正弦函数图像。

基本形式正弦曲线的基本形式可以表示为： y=Asin(B(x−C))+D
圆的极坐标公式

圆的极坐标公式描述了圆在极坐标系中的数学表达。极坐标系是一种二维坐标系统，其中每个点的位置由一个半径（r）和一个角度（θ）确定，其中半径是从原点到点的距离，角度是从正x轴到点的连线与正x轴的夹角。

基本形式

对于一个圆心位于原点（0,0）的圆，其半径为 𝑅圆的极坐标方程可以表示为： r(θ)=R 这里，𝑟是从原点到圆上任意一点的距离，θ 是从正x轴逆时针测量的角度，单位通常是度或弧度。

Just do it!

现在我们把难点梳理出来后又有了解决难点的神兵利器！接下来只需要跟着我一步一步来完成上述的效果！

如何做一个不规则圆形！

这种不规则的圆形我们普通的html元素是非常难实现的，所以我们第一考虑的就应该是动态svg！svg本身的定义就是:

矢量图形：SVG使用数学方程来定义图形，如直线、曲线、多边形等。这意味着它们可以无限放大而不失清晰度。

既然是通过数学方程来定义图形，那自然是可以通过数学方程来定义不规则圆形！观察效果图我们能发现基本图形是由一个圆形过渡到有五个突出的不规则形状。

如果忽略了动画效果形状其实就是由五个扇形组成！

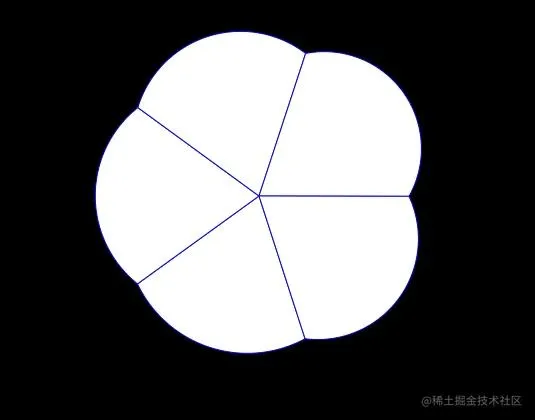
那么问题就变得简单了！，我们设置五个path并把每个path的路径都设置为扇形! 简单复习一下path的d属性值

命令	描述	参数示例
`M` 或 `m`	移动到指定点，��绘制	`M 100 200` 或 `m 30 50`
`L` 或 `l`	绘制直线到指定点	`L 200 300` 或 `l 40 50`
`H` 或 `h`	绘制水平线到指定x坐标	`H 150` 或 `h -20`
`V` 或 `v`	绘制垂直线到指定y坐标	`V 100` 或 `v -30`
`C` 或 `c`	绘制三次贝塞尔曲线	`C 100 100 200 200 300 300`
`S` 或 `s`	绘制平滑三次贝塞尔曲线	`S 200 200 300 300`
`Q` 或 `q`	绘制二次贝塞尔曲线	`Q 100 100 200 300`
`T` 或 `t`	绘制平滑二次贝塞尔曲线	`T 300 300`
`A` 或 `a`	绘制椭圆弧	`A 50 50 0 0 1 200 300`
`Z` 或 `z`	关闭路径，回到起始点	`Z` 或 `z`
数字	坐标点或控制点的坐标值	例如 `100 200`

可以看到A的作用是绘制椭圆形，也就是我们需要的命令，A或a命令的基本格式如下：

A rx ry x-axis-rotation large-arc-flag sweep-flag x y

rx 和 ry 是弧线的x轴和y轴半径。
x-axis-rotation 是椭圆的x轴相对于当前坐标系的旋转角度，单位是度（deg）。
large-arc-flag 是一个布尔值，用来指定弧线的长度。值为0表示较短的弧，值为1表示较长的弧。
sweep-flag 是另一个布尔值，用来指定绘制弧线的方向。值为0表示顺时针方向，值为1表示逆时针方向。
x 和 y 是弧线结束点的坐标（对于大写A）。

举个例子！

 1
 2<svg
 3        id="svg"
 4        width="500"
 5        height="500"
 6        version="1.1"
 7        xmlns="http://www.w3.org/2000/svg">
 8
 9    <path fill="white" d="M250,250 L250,100 A150,150 0 0,1 400,250 Z"/>
10
11</svg>
12

可以看到我们首先使用M命令移动到中心点，然后使用L命令画出了一个半径150的圆形半径，最后使用A命令并且让rx,ry等于圆形的半径150，此时就会出现一个1/4圆，如果我们让rx,ry不等于半径就会发生突起效果！

 1<svg
 2        id="svg"
 3        width="500"
 4        height="500"
 5        version="1.1"
 6        xmlns="http://www.w3.org/2000/svg">
 7
 8    <path fill="white" d="M250,250 L250,100 A100,100 0 0,1 400,250 Z"/>
 9
10</svg>

明白了突起效果的原理我们就可以回答第一个难题了，如何做一个不规则突起的圆！答案是利用A命令，并且动态改变rx,ry使其不等于圆形的半径。

但是此时会面临一个数学问题，一个圆形需要五个扇形组成，扇形A命令的x,y应该怎么算出来，注意这里不是rx,ry!此时就需要我们的神兵利器之一圆的极坐标公式出场了！

对于一个圆心位于原点（0,0）的圆，其半径为 𝑅圆的极坐标方程可以表示为：

r(θ)=R 这里，𝑟是从原点到圆上任意一点的距离，θ 是从正x轴逆时针测量的角度，单位通常是度或弧度。极坐标公式为：

x=rcos(θ)

y=rsin(θ)

我们已知r=150,θ = 360 / 5 = 72°，自然可以算出来五个扇形的x,y！

 1
 2<svg
 3        id="svg"
 4        width="500"
 5        height="500"
 6        version="1.1"
 7        xmlns="http://www.w3.org/2000/svg">
 8
 9        <path class="path" d="M250,250 L400,250 A150,150 0 0,1 296.3525491562421,392.658477444273 L250,250 A 0,0 0 0,1 250,250 Z" fill="white"></path>
10
11        <path class="path" d="M250,250 L296.3525491562421,392.658477444273 A150,150 0 0,1 128.6474508437579,338.167787843871 L250,250 A 0,0 0 0,1 250,250 Z" fill="white"></path>
12
13        <path class="path" d="M250,250 L128.6474508437579,338.167787843871 A150,150 0 0,1 128.64745084375787,161.83221215612906 L250,250 A 0,0 0 0,1 250,250 Z" fill="white"></path>
14
15        <path class="path" d="M250,250 L128.64745084375787,161.83221215612906 A150,150 0 0,1 296.3525491562421,107.34152255572695 L250,250 A 0,0 0 0,1 250,250 Z" fill="white"></path>
16
17        <path class="path" d="M250,250 L296.3525491562421,107.34152255572695 A150,150 0 0,1 400,249.99999999999997 L250,250 A 0,0 0 0,1 250,250 Z" fill="white"></path>
18
19</svg>
20

此时有一个完美的圆形之后，我们只要考虑如何动态改变A命令的rx,ry就可以了，观察效果会发现，在不规则的圆形成后，其实整个形状是在一定范围内不断重复循环并且带上了一些旋转效果，此时应该请出我们另一个神兵利器。

看到这种在一定范围内不断重复的效果，我们应该首先想到就是利用正弦曲线循环往复的特性来完成

正弦曲线的基本形式可以表示为：y=Asin(B(x−C))+D

带入我们实际情况来看

rx,ry = y
A = 振幅
D = 初始偏移量
B = 频率

为了让效果更灵动一点，我这边把频率设置成随机数了，大家可以自行尝试喜欢的频率,精简后的代码如下:

 1window.SineWaveGenerator = class SineWaveGenerator {
 2
 3    phase = Math.PI / 2
 4
 5    constructor(frequency, amplitude, offset) {
 6        this.frequency = frequency
 7        this.amplitude = amplitude
 8        this.offset = offset
 9    }
10
11
12    calculateValue(currentTime) {
13        const currentFrequency = this.frequency
14        const currentAmplitude = this.amplitude
15        const currentOffset = this.offset
16        // 计算并返回当前的正弦波值
17        return currentAmplitude * Math.sin(currentFrequency * currentTime + this.phase) + currentOffset
18    }
19
20}
21
22const min = 0.002
23const max = 0.004
24const circleSineWaveGenerator = []
25for (let i = 0
26    const f = this.getRandomBetween(min, max)
27    const s = new window.SineWaveGenerator(f, 27.5, 122.5)
28    circleSineWaveGenerator.push(s)
29}
30
31const points = circle.calculateValue(angle, xy)
32points.forEach((f, i) => circlePaths[i].setAttribute('d', f))
33

至此第一个问题就解决了。

溶解粘滞效果

关于溶解粘滞的效果，我们其实可以参考Coco大佬的一篇文章你所不知道的 CSS 滤镜技巧与细节核心是利用了两个滤镜:

filter: blur()：给图像设置高斯模糊效果。
filter: contrast()：调整图像的对比度。

这两个滤镜结合的时候我们会发现产生了神奇的粘滞效果

我们的方案是使用svg,是否可以直接使用上述的方案呢，答案是不行的😢，但是！我们有自己的神兵利器，svg滤镜！

SVG滤镜（Scalable Vector Graphics Filters）是SVG（可缩放矢量图形）规范的一部分，用于对SVG图形应用各种视觉效果。SVG滤镜允许开发人员和设计师创建复杂的图形效果，比如模糊、阴影、颜色变化等，而无需使用位图图像

既然css可以通过blur结合contrast滤镜来完成粘滞效果，我们的svg滤镜是否有类似的功能呢，答案是YES！💕

feGaussianBlur 是一种模糊滤镜，它根据高斯函数对图像进行模糊处理。高斯模糊是一种非常流行的图像处理技术，常用于减少图像噪声或创建柔和的边缘效果。
feColorMatrix 滤镜允许你对图像的颜色和 Alpha 通道进行矩阵变换。这可以用来调整颜色平衡、对比度、亮度等，或者实现更复杂的颜色效果。

这两个滤镜结合可以实现和CSS滤镜完全一致的效果！，滤镜的使用方法也可以参考有意思！强大的 SVG 滤镜本篇不再详细赘述。

因为要用到滤镜此时我们的svg结构需要有所调整，需要多加一层g标签来保证滤镜的效果

 1
 2<svg id="svg" width="500" height="500" version="1.1" xmlns="http://www.w3.org/2000/svg">
 3
 4    <defs>
 5        <filter id="goo">
 6            <feGaussianBlur ...></feGaussianBlur>
 7            <feColorMatrix ...></feColorMatrix>
 8        </filter>
 9    </defs>
10    <g filter="url(#goo)">
11        <path ...></path>
12        <path ...></path>
13        <path ...></path>
14        <path ...></path>
15        <path ...></path>
16    </g>
17</svg>
18

此时我们的准备工作就已经全部完成了，接下来需要把圆形变为分散的音柱结构！这种形变也是svg所擅长的！我们只需要计算出音柱的各个坐标信息并动态修改即可！

 1
 2    canvasWidth = 500
 3    canvasHeight = 500
 4
 5    width = 300
 6    height = 300
 7
 8    initStartX
 9    initStartY
10
11    audioWidth = 0
12    audioSpace = 4
13    audioCount = 4
14
15    constructor(paths) {
16
17        this.circlePaths = paths
18
19        // 音柱的开始x
20        this.initStartX = (this.canvasWidth - this.width) / 2
21
22        // 音柱的开始y
23        this.initStartY = this.canvasHeight / 2
24        
25        // 音柱的宽度
26        this.audioWidth = (this.width - (this.audioCount - 1) * this.audioSpace) / this.audioCount
27
28    }
29

此时我们已经计算出了所有音柱的坐标信息，这里有一点需要注意，圆形是由五个扇形组成，音柱是由四个圆柱组成，所以我们需要两片扇形共用一个圆柱的坐标信息!

 1
 2decomposerAnimation(timeStart) {
 3
 4        let startX = this.initStartX
 5
 6        const pathSteps = []
 7
 8        const tempStartX = []
 9        const tempStartY = []
10        const tempHeight = []
11
12
13        for (let i = 0
14            // 让音柱y轴有一些偏差效果更自然
15            let startY = i > 1 ? this.initStartY + Math.abs((4 - i) * 20) : this.initStartY + 80
16            // 让音柱高度有一些偏差效果更自然
17            const h = i > 1 ? 30 : 20
18            const p = this.getDecomposePath(startX, startY, h)
19            pathSteps.push(p)
20            tempStartX.push(startX)
21            tempStartY.push(startY)
22            tempHeight.push(h)
23            startX += (this.audioWidth + this.audioSpace)
24        }
25
26        let startPaths = this.circlePaths.reduce((p, c) => [...p, this.execPath(c.getAttribute('d'))], [])
27
28        let endPaths = Array.from({length: this.circlePaths.length}).map((value, index) => this.execPath(this.getPath(index, pathSteps)))
29
30        const animation = () => {
31            const currentTime = performance.now()
32            const timeElapsed = currentTime - timeStart
33            const progress = Math.min(timeElapsed / this.decomposerDuration, 1)
34            this.circlePaths.forEach((f, i) => f.setAttribute('d', this.calePathProgress(startPaths[i], endPaths[i], progress)))
35            if (progress < 1) requestAnimationFrame(() => animation(timeStart))
36            // else requestAnimationFrame(timeStart => this.translateAnimation(timeStart))
37        }
38
39        animation()
40
41}
42

此时我们可以发现，粘滞效果已经实现了，但是我们的需求是分裂后就不要在保持粘滞效果了，所以我们在执行分裂动画的时候也需要动态调整两个滤镜的参数!

 1
 2     const blur = document.getElementById('blur')
 3     const matrix = document.getElementById('matrix')
 4     
 5     // 动态过渡到没有粘滞效果
 6     const filterAnimation = () => {
 7         const currentTime = performance.now()
 8         const timeElapsed = currentTime - timeStart
 9         const progress = Math.min(timeElapsed / this.filterDuration, 1)
10         const blurValue = Math.max(15 - (15 * progress), 0)
11         const v1 = 26 - (25 * progress)
12         const v2 = -7 + (7 * progress)
13         blur.setAttribute('stdDeviation', blurValue.toString())
14         const values = `1 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 ${v1} ${v2}`
15         matrix.setAttribute('values', values)
16     }
17

此时我们的问题二也有了答案，如何做溶解粘滞效果，利用svg滤镜！同时动态调整滤镜参数

音柱抖动效果

ChatGPT这个音柱的抖动肯定是根据声音输入来动态改变的，咱们只是模仿效果，只需要观察效果的核心原理即可，也就是这个圆柱在一定的高度重复抖动！看到重复我们就应该知道又要用到我们的老朋友正弦函数来帮忙啦！

 1
 2        const sineDuration = 2000
 3        const resetDuration = 200
 4
 5        let startPaths = []
 6        let endPaths = []
 7
 8        const sineAnimation = (timeStart) => {
 9
10            const currentTime = performance.now()
11            const timeElapsed = currentTime - timeStart
12            const progress = Math.min(timeElapsed / sineDuration, 1)
13
14            const handleStart = (f, i) => {
15                const progress = Math.min(timeElapsed / duration[i], 1)
16
17                const initialFrequency = Math.PI * 0.018
18                const finalFrequency = Math.PI * 0.008
19
20                // 动态计算当前振幅范围
21                const currentMinHeight = lerp(range[i][0], range[i][2], progress)
22                const currentMaxHeight = lerp(range[i][1], range[i][3], progress)
23
24                // 使用正弦函数计算当前高度
25                const heightRange = (currentMaxHeight - currentMinHeight) / 2
26                const averageHeight = (currentMaxHeight + currentMinHeight) / 2
27                const frequency = lerp(initialFrequency, finalFrequency, progress)
28                const currentHeight = averageHeight + heightRange * Math.sin(frequency * timeElapsed)
29
30                const {x, y} = this.getDecomposePathXY(f.getAttribute('d'))
31                f.setAttribute('d', this.getDecomposePath(x, y, currentHeight))
32            }
33
34
35            this.circlePaths.forEach(handleStart)
36
37            if (progress < 1) {
38                requestAnimationFrame(() => sineAnimation(timeStart))
39                return
40            }
41
42            startPaths = this.circlePaths.reduce((p, c) => [...p, this.execPath(c.getAttribute('d'))], [])
43
44            endPaths = this.circlePaths.map(v => {
45                const {x, y} = this.getDecomposePathXY(v.getAttribute('d'))
46                return this.execPath(this.getDecomposePath(x, y, 0))
47            })
48
49            requestAnimationFrame(timeStart => resetAnimation(timeStart))
50
51        }
52

核心就是利用正弦函数来不断的改变我们音柱的高度！

融合拓展效果

终于到我们最后一个效果了！经过了问题二，我们应该知道融合效果的实现方式是根据svg滤镜来实现的，在效果二最后我们把滤镜过渡到了没有粘滞效果的状态，此时我们应该重新过渡到有粘滞效果的状态！

 1
 2  const blur = document.getElementById('blur')
 3  const matrix = document.getElementById('matrix')
 4  const filterAnimation = (timeStart) => {
 5        const currentTime = performance.now()
 6        const timeElapsed = currentTime - timeStart
 7        const progress = Math.min(timeElapsed / this.filterDuration, 1)
 8        const blurValue = Math.min(15 * progress, 15)
 9        const v1 = 1 + (25 * progress)
10        const v2 = 0 - (7 * progress)
11        blur.setAttribute('stdDeviation', blurValue.toString())
12        const values = `1 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 ${v1} ${v2}`
13        matrix.setAttribute('values', values)
14    }
15

大功告成了么？并不！如果我们仅仅只是把粘滞的效果恢复同时把四个音柱的坐标恢复成最开始的圆形坐标时会发现效果如下:

虽然最后融合成了一个圆，但是和ChatGPT的效果不一样，融合的过程有一些扭曲。此时我们要使用一个小小的障眼法！还记得在问题二中我们隐藏了一个扇形，此时就应该派上用场了。

思路如下：

藏一个音柱并改成椭圆结构藏在最后面，剩下的四个音柱往中心聚拢，同时中心的两个音柱高度变化，藏在后面的椭圆结构撑起来变成一个圆！

完整代码

结语

OK，整个效果做下来，我们捋清了filter的使用，一些数学公式的实际运用，希望大家能看的开心，学的开心！